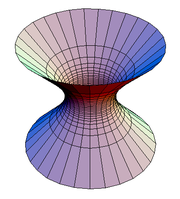
Hyperboloid
|
|
In mathematics, a hyperboloid is a quadric, a type of surface in three dimensions, described by the equation:
- <math>{x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}=1<math> (hyperboloid of one sheet),
or
- <math>{x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}=-1<math> (hyperboloid of two sheets)
If, and only if, <math>a=b<math>, it is a hyperboloid of revolution. A hyperboloid of one sheet can be obtained by revolving a hyperbola around its transversal axis. Alternatively, a hyperboloid of two sheets of axis AB is obtained as the set of points P such that AP-BP is a constant, AP being the distance between A and P. A and B are then called the foci of the hyperboloid. A hyperboloid of two sheets can be obtained by revolving a hyperbola around its focal axis.
A hyperboloid of one sheet is a ruled surface; if it is a hyperboloid of revolution, it can also be obtained by revolving a line about a skew line.
A degenerate hyperboloid is of the form:
- <math>{x^2 \over a^2} + {y^2 \over b^2} - {z^2 \over c^2}=0;<math>
if a = b then this will give a cone, if not then it gives an elliptical cone.
See also: ellipsoid, paraboloid.de:Hyperboloid es:Hiperboloide fr:Hyperbolo´de it:Iperboloide nl:Hyperbolo´de pl:Hiperboloida