Perspective projection distortion
|
|
Perspective projection distortion is an error introduced in drawing when images are created by the use of "projectors". Projectors are imaginary constructs which aid in the production of real images. See graphical projection, orthographic projection, and multiview without rotation. In perspective projection, nonparallel projectors are imagined to emanate from all points of an object and are concurrent at a point. These projectors create an imaginary image where they intersect an imaginary plane of projection. This image represents the object as seen by the eye from the point of concurrence. The image is then reproduced onto a planar surface (e.g. paper) by geometric protocols. Understanding this image requires a familiarity with these protocols.
The chances of the casual viewer viewing the final real-world image from precisely the point of concurrence (station point), where distortion disappears, are minute. Therefore, the viewer is presented with an intrinsic distortion, the amount of which depends on his chance distance from the theoretical station point. This phenomenon is addressed below.
A second source of distortion is the (healthy) eye itself. The eye does not perceive the true geometry that exists in nature. The reason for this phenomenon and the correct way to project the image beheld by the eye is also addressed below.
| Contents |
Why perspective distortion occurs
Picture_plane_projection.png
Picture_plane_ortho_view.png
The physiological basis of foreshortening went undefined until the year 1000 when the Arabian mathematician and philosopher, Alhazen, in his Perspectiva, first explained that light projects conically into the eye. A method for presenting foreshortened geometry systematically on a plane surface was unknown for another 300 years. The artist Giotto may have been the first to recognize that the image beheld by the eye is distorted---that to the eye, parallel lines appear to intersect (in the manner of receding railroad tracks) whereas in "undistorted" nature, they do not. One of the first uses of perspective was in Giotto’s ‘Jesus Before the Caïf’, more than 100 years before Brunelleschi’s perspectival demonstrations galvanized the widespread use of convergent perspective of the Renaissance proper.
Artificial perspective projection is the name given by Leonardo da Vinci to what today is called classical perspective projection. Natural perspective projection is the name given by Leonardo to the projection that produces the image beheld by the human eye. Both types of projection involve a distortion; parallel lines never intersect in nature, but they always intersect in perspective projections, with the rare exception wherein both the surface of projection is planar and an object plane is spatially parallel to the plane of projection.
The difference between the images of the same object produced by artificial perspective projection and by natural perspective projection is called perspective distortion. This article preserves the usage of the Leonardo designation, artificial projection, in place of classical projection so as to acknowledge that Leonardo recognized that classical perspective projection indeed does produce an image different from that beheld by the eye.
Distortion caused by projection
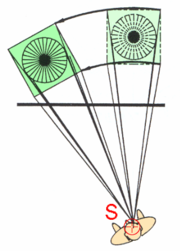
Figures 1-3 show the principle of an artificial perspective projection. The artificial perspective projection image appears upon the projection plane (P). Imagine a human eye is placed at the station point (S). This human eye views both the object and the image of the object as if the projection plane did not exist. That is to say, to the eye, from the station point (only) the image of the object is indistinguishable from the object itself.
In the special case---and the only instance---in which an artificial perspective image appears the same to the eye as does a natural perspective image, the eye must view the artificial perspective image from precisely the spatial station point, i.e., from the station point as it is located in actual space.
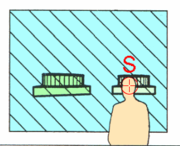
To illustrate, Figures 4-6 show the object in Figure 1 to be pivoted about the imagined eye to a new position, while maintaining its original face toward the eye. The new object image will appear the same to the eye as at the original position. But take note that the artificial projection image of the object in its new position is different from the original artificial projection image. In other words, the two artificial projection images are different because the angles of the respective projectors as they intersect the picture plane are different. The pivoted image thus exhibits an obvious distortion over the unpivoted image. However, both images appear identical to the eye because the eye is located at the station point and the angle of viewing from the station point to the new image cancels out the new angles of the projectors. Or to say it another way, by looking at the distorted image in a distorted (skewed) direction the image appears undistorted to the eye. From Figure 6 it is intuitively apparent that the image viewed from any position other than the Station point appears distorted.
Distortion still caused by projection
It is not immediately apparent on a day-to-day basis that there is distortion in the image beheld by the eye because we experience nothing else visually throughout our lives, but on reflection there is an obvious contradiction that has not been fully explained: Why do straight parallel lines in space appear to intersect twice? The following thought experiment illustrates the contradiction:
Imagine that on an infinite plane there is an infinitely long and infinitely straight railroad, and that you are standing between the parallel rails. As you peer down the track in one direction the rails appear to intersect (on the horizon). As you peer in the opposite direction they again appear to intersect. You look at your feet and the rails are far apart. It logically follows that if they intersect, as it would appear, one or both of the rails are curved. To determine which, you put your eye onto one rail and sight down it. You discover it is straight in the sighted direction. You then sight down the same rail in the opposite direction. You discover it is straight also in the opposite direction. It logically follows, then, that the other rail must be curved. You similarly test the other rail and discover it too is straight. How can this happen?
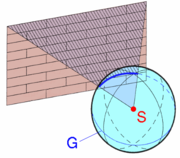
The explanation lies in that they do not actually intersect, but only appear to. If you take a flat photograph in one direction, they both appear straight, and to intersect in one place, and if you take a flat photograph in the other direction, they both intersect in a different place, but it is not possible to take a normal flat photograph which shows them intersecting both places at once, since the two apparent intersections are in opposite directions and an infinite distance away (the tracks appear infinitely thin at an infinite distance). A way to avoid the problem of the tracks only intersecting when you look straight at them is to use a spherical surface of projection with the observer in the centre. That way, the surface of projection is rotationally invariant, so one can see both intersections at once. Note that the all straight lines are projected as great semicircles on the sphere. Since the projected straight lines are no longer straight when using a projection that shows both intersections, there is no contradiction. Also, note that the lines end where they meet. Figure 7 illustrates this process. The station point (S) in this situation is located in the center of the picture sphere (P). The brick wall in the background serves as a representative object to be projected. This produces a more accurate simulation of that which the eye beholds.
Picture_sphere.png
Picture_sphere_bottom_intersection.png
To understand the process, be reminded that:
- perspective projections of straight lines that are in space, through the center of a sphere, projectively create great semicircles upon the picture sphere, and
- these great semicircles appear as straight lines when viewed from the center of the sphere.
These are the reasons why the natural perspective projection of the rails of our thought experiment actually produces two intersecting (at opposite poles of the sphere) semicircular images upon the picture Sphere (retina) and yet appear straight when viewed from the center. For this to be consistent with our normal vision requires that we either cannot see in two opposite directions at once, or that the retina (macula?) is not a single flat plane in shape, or that there is a lens in the eye. The second two possibilities apply - the retina is not flat (similar to spherical for humans, in fact), and there are lenses in the eye. The image is inverted at the focal point before striking the retina, but which has no bearing on the theory.
Therefore, to produce the image which the retina beholds, using projective geometry techniques, it may be convenient to substitute a spherical surface of projection for a plane of projection, i.e., use a "picture sphere" rather than a "picture plane" and place the eye, or "station point," at the center of the picture sphere. Alternatively, a box may be used instead of a sphere.
For a step-by-step example, see Figures 8-12.
Figure 8 shows that the perspective projection of the horizontal top line of the wall intersects at the retina (actually, in true life, at the focal point slightly in front of the retina and from where it is inverted). The intersecting lines define a plane that intersects the sphere of projection in a great circle (G).
Figure 9 shows the projection of the horizontal bottom line of the wall and its great circle of intersection (H).
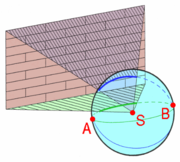
Figure 10 shows that the two great circles of intersection intersect at points A and B. The two points of intersection are two (vanishing) points on the horizon line of the plane of the wall as seen from the center of the picture sphere. The points of intersection are analogous to the two points of intersection as one peers down a railroad track in both directions; a viewer situated at the station point S looking in the direction of point A would see the lines of the wall converge there; the same is true of point B.
Figure 11 shows a similar determination of the two vanishing points C and D for the spatially vertical lines of the wall. For example, if the wall in this situation were a very tall building, a viewer looking up towards point C would see the sides of the building converge there. Note that this correct "four point" perspective is analogous to the distorted "three point" perspective of classical perspective projection. The region of the picture sphere upon which the image of the brick wall would be projected is shaded in green.
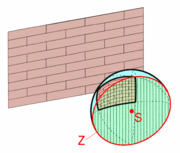
The horizon line of the wall in all directions is determined by a plane intersecting the four given vanishing points A, B, C, and D. Figure 12 demonstrates that a horizon line Z can be determined by vanishing points only; a viewer at S looking towards any point along the circumference of Z would perceive that point as part of the horizon, relative to the plane of the wall.
Conclusion
A spherical projection surface is required in order to represent without rotationally-dependent distortion the image beheld by the eye. (This does not conclusively demonstrate that the retina itself is spherical in shape.) As it is impossible for an image on a sphere to be rectified without distortion onto a plane surface, the image that the eye beholds may never be represented without using a different distortion to the one used on a plane surface. An analogy is the impossibility of representing the surface of the earth without distortion on a flat surface (map). Note that it logically follows that all photography distorts the image that is beheld by the eye because the film surface is flat in the manner of the picture plane. While artifactual characteristics of a camera lens may aggravate the distortion, that distortion is only ancillary to the fundamental cause of distortion described here. This is demonstrated with a pinhole camera which has no lens but which produces the same distortion as described herein.