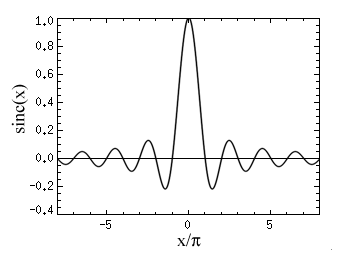
Sinc function
|
|
In mathematics, the sinc function (for sinus cardinalis), also known as the interpolation function, filtering function or the first spherical Bessel function <math>j_0(x)<math>, is the product of a sine function and a monotonically decreasing function. It is defined by:
- <math>\textrm{sinc}(x)
= \left\{ \begin{matrix} \frac{\sin(x)}{x}&:~x\ne 0 \\ \\ 1 &:~x=0 \end{matrix} \right. <math>
The sinc function is sometimes defined as simply sin(x)/x. The function sin(x)/x has a removable singularity at zero, so that, by L'H˘pital's rule we have:
- <math>\lim_{x\to 0} \frac{\sin(x)}{x}=1.\,<math>
The above definition for the sinc function is preferred since it removes this singularity and yields a function which is analytic everywhere.
The normalized sinc function is defined as:
- <math>\mathrm{sinc}_N(x) = \textrm{sinc}(\pi x)\,<math>
and, as its name implies, is normalized to unity
- <math>\int_{-\infty}^\infty \mathrm{sinc}_N(x)\,dx = 1.<math>
This integral must necessarily be regarded as an improper integral; it cannot be taken to be a Lebesgue integral because
- <math>\int_{-\infty}^\infty \left|\mathrm{sinc}_N(x)\right|\,dx = \infty.<math>
The normalized sinc function also has the important infinite product
- <math>\mathrm{sinc}_N(x) = \prod_{n=1}^\infty \left(1 - \frac{x^2}{n^2}\right).<math>
We also have an expression in terms of the gamma function, as
- <math>\mathrm{sinc}_N(x) = \frac{1}{\Gamma(1+x)\Gamma(1-x)} = \frac{1}{x! (-x)!}.<math>
Because of its usefulness, the normalized sinc function is sometimes simply called the sinc function and written sinc(x).
The sinc function oscillates inside an envelope of ±1/x. The Fourier transform of the sinc function can be expressed in terms of the rectangular function:
- <math>\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty \textrm{sinc}(x)e^{-ikx}\,dx=
\sqrt{\frac{\pi}{2}}~\textrm{rect}(k/2)<math>
In the language of distributions, the sinc function is related to the delta function δ(x) by
- <math>\lim_{a\rightarrow 0}\frac{1}{\pi a}\textrm{sinc}(x/a)=\delta(x).<math>
This is not an ordinary limit, since the left side does not converge. Rather, it means that
- <math>\lim_{a\rightarrow 0}\int_{-\infty}^\infty \frac{1}{\pi a}\textrm{sinc}(x/a)\varphi(x)\,dx
=\int_{-\infty}^\infty\delta(x)\varphi(x)\,dx = \varphi(0),
<math>
for any smooth function <math>\varphi(x)<math> with compact support.
In the above expression, as a approaches zero, the number of oscillations per unit length of the sinc function approaches infinity. Nevertheless, the sinc function always oscillates inside an envelope of ±1/x, regardless of the value of a. This contradicts the informal picture of δ(x) as being zero for all x except at the point x=0 and illustrates the problem of thinking of the delta function as a function rather than as a distribution. A similar situation is found in the Gibbs phenomenon.
Applications of the sinc function are found in digital signal processing, communication theory, control theory, and optics.