Special relativity
|
|
A simple introduction to this subject is provided in Special relativity for beginners
Special relativity(SR) or the special theory of relativity is the physical theory published (http://www.fourmilab.ch/etexts/einstein/specrel/www/) in 1905 by Albert Einstein. It replaced Newtonian notions of space and time and incorporated electromagnetism as represented by Maxwell's equations. The theory is called "special" because it is a special case of Einstein's theory of relativity where the effects of gravity can be ignored. Ten years later, Einstein published the theory of general relativity which incorporates gravitation.
| Contents |
History and motivation
Main article: History of special relativity
The principle of relativity was introduced by Galileo. Overturning the old absolutist views of Aristotle, it held that motion, or at least uniform motion in a straight line, only had meaning relative to something else, and that there was no absolute reference frame by which all things could be measured.
The principle of relativity seemed to work well for everyday phenomena involving solid objects, but light was still problematic. Mechanical waves travel in a medium, and so it was assumed for light. This hypothetical medium was called the "luminiferous aether." The idea of an aether seemed to reintroduce the idea of a detectable absolute frame of reference, one that is stationary with respect to the aether.
After Maxwell's unification of light, electricity, and magnetism, and after experimental evidence such as Michelson-Morley experiment, a consensus emerged that the speed of light does not vary with the speed of the observer, and the speed of light must be invariant (the same) for all observers. This seemed to further conflict with the principle of relativity. Hendrik Lorentz proposed a resolution by postulating an aether theory in which objects and observers travelling with respect to a stationary aether underwent a physical shortening (Lorentz-Fitzgerald contraction) and a change in temporal rate (time dilation). Poincaré's version of the relativity principle (1904) went: "The laws of physical phenomenons must be the same, whether for a fixed observer, as also for one dragged in a motion of uniform translation, so that we do not and cannot have any mean to discern whether or not we are dragged in a such motion."
Einstein's contribution was, inter alia, to derive Lorentz's equations from a more fundamental principle without assuming the presence of an aether. Under Special Relativity, the seemingly complex transformations of Lorentz and Fitzgerald derived cleanly from simple geometry and the Pythagorean theorem. The original title for his theory was (translated from German) "On the Electrodynamics of Moving Bodies". Max Planck first suggested the term "relativity" to highlight the notion of transforming the laws of physics between observers moving relative to one another.
Postulates
Main article: Postulates of special relativity
1. First postulate (principle of relativity)
- The laws of electrodynamics and optics will be valid for all frames in which the laws of mechanics hold good.
- Every physical theory should look the same mathematically to every inertial observer.
- The laws of physics are independent of location space or time.
2. Second postulate (invariance of c)
- The speed of light in vacuum, commonly denoted c, is the same to all inertial observers, is the same in all directions, and does not depend on the velocity of the object emitting the light. When combined with the First Postulate, this Second Postulate is equivalent to stating that light does not require any medium (such as "aether") in which to propagate.
Status
Main article: Status of special relativity
Special relativity is only accurate when gravitational effects are negligible or very weak, otherwise it must be replaced by general relativity. At very small scales, such as at the Planck length and below, it is also possible that special relativity breaks down, due to the effects of quantum gravity. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is now universally accepted by the physics community and experimental results which appear to contradict it are widely believed to be due to unreproducible experimental error.
Because of the freedom one has to select how one defines units of length and time in physics, it is possible to make one of the two postulates of relativity a tautological consequence of the definitions, but one cannot do this for both postulates simultaneously, as when combined they have consequences which are independent of one's choice of definition of length and time.
Special relativity is mathematically self-consistent, and is also compatible with all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields). However special relativity is incompatible with several earlier theories, most notably Newtonian mechanics. See Status of special relativity for a more detailed discussion.
A number of experiments have been conducted to test special relativity against rival theories. These include:
- The Michelson-Morley experiment disproved the possibility of ether drift, and tested the directional invariance of the speed of light
- Hamar experiment - obstruction of ether flow
- Trouton-Noble experiment - torque on a capacitor
- Kennedy-Thorndike experiment - time contraction
- Rossi-Hall experiment - spacetime contraction's effects on a fast-moving particle's half-life
- Experiments to test emitter theory demonstrated that the speed of light is independent of the speed of the emitter.
Consequences
Main article: Consequences of Special Relativity
Special relativity leads to different physical predictions than Galilean relativity when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything humans encounter that some of the effects predicted by relativity are initially counter intuitive.
- The time lapse between two events is not invariant from observer to another, but is dependent on the relative speeds of the observers' reference frames. (See Lorentz transformation equations)
- Two events that occur simultaneously in different places in one frame of reference may occur at different times in another frame of reference (lack of absolute simultaneity).
- The dimensions (e.g. length) of an object as measured by one observer may differ from the results of measurements of the same object made by another observer. (See Lorentz transformation equations)
- The twin paradox concerns a twin who flies off in a spaceship travelling near the speed of light. When he returns he discovers that his twin has aged much more rapidly than he has (or he aged more slowly).
- The ladder paradox involves a long ladder travelling near the speed of light and being contained within a smaller garage.
Lack of an absolute reference frame
Special Relativity rejects the idea of any absolute ('unique' or 'special') frame of reference; rather physics must look the same to all observers travelling at a constant velocity (inertial frame). This 'principle of relativity' dates back to Galileo, and is incorporated into Newtonian Physics. In the late 19th Century, some physicists suggested that the universe was filled with a substance known as "aether" which transmited Electromagnetic waves. Aether constituted an absolute reference frame against which speeds could be measured. Aether had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, those waves could interact with matter, yet it offered no resistance to bodies passing through it. The results of various experiments, including the Michelson-Morley experiment, suggested that the Earth was always 'stationary' relative to the Aether - something that is difficult to explain. The most elegant solution was to discard the notion of Aether and an absolute frame, and to adopt Einstein's postulates.
Mass, momentum, and energy
In addition to modifying notions of space and time, special relativity forces one to reconsider the concepts of mass, momentum, and energy, all of which are important constructs in Newtonian mechanics. Special relativity shows, in fact, that these concepts are all different aspects of the same physical quantity in much the same way that it shows space and time to be interrelated.
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses conservation laws. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple thought experiments using the Newtonian definitions of momentum and energy one sees that these quantities are not conserved in SR. One can rescue the idea of conservation by making some small modifications to the definitions to account for relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
Given an object of invariant mass m_0 traveling at velocity u the energy and momentum are given by
- <math>E = \gamma m_0 c^2 \,\!<math>
- <math> p = \gamma m_0 u \,\!<math>
where γ (the Lorentz factor) is given by
- <math>\gamma = \frac{1}{\sqrt{1 - u^2/c^2}} \,\!<math>
and c is the speed of light. The term γ occurs frequently in relativity, and comes from the Lorentz transformation equations. The energy and momentum can be related through the formula
- <math> E^2 - (p c)^2 = (m_0 c^2)^2 \,\!<math>
which is referred to as the relativistic energy-momentum equation. These equations can be more succinctly stated using the four-momentum <math>P^a<math> and the four-velocity <math>U^a<math> as
- <math>P^a = m_0 U^a<math>
which can be viewed as a relativistic analogue of Newton's second law.
For velocities much smaller than those of light γ can be approximated using a Taylor series expansion and one finds that
- <math> E \approx m_0 c^2 + \begin{matrix} \frac{1}{2} \end{matrix} m_0 u^2 \,\!<math>
- <math> p \approx m_0 u \,\!<math>
Barring the first term in the energy expression (discussed below), these formulas agree exactly with the standard definitions of Newtonian kinetic energy and momentum. This is as it should be, for special relativity must agree with Newtonian mechanics at low velocities.
Looking at the above formulas for energy, one sees that when an object is at rest (u = 0 and γ = 1) there is a non-zero energy remaining:
- <math>E = m_0 c^2 \,\!<math>
This energy is referred to as rest energy. The rest energy does not cause any conflict with the Newtonian theory because it is a constant and, as far as kinetic energy is concerned, it is only differences in energy which matter.
Taking this formula at face value, we see that in relativity, mass is simply another form of energy. This formula becomes important when one measures the masses of different atomic nuclei. By looking at the difference in masses, one can predict which nuclei have extra stored energy which can be released by nuclear reactions, providing important information which was useful in the development of the nuclear bomb. The implications of this formula on 20th century life has made it one of the most famous equations in all of science.
On mass
Introdutory physics courses and some older textbooks on special relativity sometimes define a so-called relativistic mass which may lead to the mistaken impression that special relativity implies the mass of a body increases as its velocity increases. This is technically incorrect from a theoretical standpoint since the first postulate was used to construct a theory in which the properties of an object are independent of any inertial frame, i.e., invariant.
Nevertheless, defining such a quantity may sometimes be useful in that doing so simplifies a calculation by restricting it to a specific frame. For example, consider an obsever who considers himself at rest and a body with an invariant mass, :<math>m_0 \!<math> moving at some velocity relative to that observer. That observer defines the relativistic mass of that body as:
- <math>m = \gamma m_0\!<math>
Note that the body does not actually become more massive, since the relativistic mass would be different for an observer in a different frame. The only mass which is observer independent is the invariant mass. When using the relativistic mass, one must always specify a velocity relative to a particular observer. Introductory textbooks sometimes use the relativistic mass because it allows the students to utilize their knowledge of Newtonian physics to gain some intuitive grasp of relativity in the frame they find most interesting - their own!
Simultaneity and causality
Special relativity holds that events that are simultaneous in one frame of reference need not be simultaneous in another frame of reference.
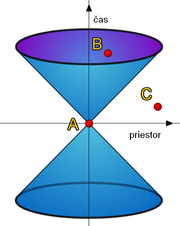
The interval AB in the diagram to the right is 'time-like'. I.e. there is a frame of reference in which event A and event B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like'. I.e. there is a frame of reference in which event A and event C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. Barring some way of traveling faster than light, it is not possible for any matter (or information) to travel from A to C or from C to A. Thus there is no causal connection between A and C.
The geometry of space-time
SR uses a 'flat' 4-dimensional Minkowski space, which is an example of a space-time. This space, however, is very similar to the standard 3 dimensional Euclidean space, and fortunately by that fact, very easy to work with.
The differential of distance(ds) in cartesian 3D space is defined as:
- <math> ds^2 = dx_1^2 + dx_2^2 + dx_3^2 <math>
where <math>(dx_1,dx_2,dx_3)<math> are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension, time, is added, with units of c, so that the equation for the differential of distance becomes:
- <math> ds^2 = dx_1^2 + dx_2^2 + dx_3^2 - c^2 dt^2 <math>
In many situations it may be convenient to treat time as imaginary (e.g. it may simplify equations), in which case <math>t<math> in the above equation is replaced by <math>i.t'<math>, and the metric becomes
- <math> ds^2 = dx_1^2 + dx_2^2 + dx_3^2 + c^2(dt')^2 <math>
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3-D space
- <math> ds^2 = dx_1^2 + dx_2^2 - c^2 dt^2 <math>
We see that the null geodesics lie along a dual-cone:
Missing image
Sr1.jpg
image:sr1.jpg
defined by the equation
- <math> ds^2 = 0 = dx_1^2 + dx_2^2 - c^2 dt^2 <math>
or
- <math> dx_1^2 + dx_2^2 = c^2 dt^2 <math>
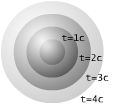
Which is the equation of a circle with r=c*dt. If we extend this to three spatial dimensions, the null geodesics are continuous concentric spheres, with radius = distance = c*(+ or -)time.
- <math> ds^2 = 0 = dx_1^2 + dx_2^2 + dx_3^2 - c^2 dt^2 <math>
- <math> dx_1^2 + dx_2^2 + dx_3^2 = c^2 dt^2 <math>
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old.", we are looking down this line of sight: a null geodesic. We are looking at an event <math>d = \sqrt{x_1^2+x_2^2+x_3^2} <math> meters away and d/c seconds in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
Missing image
Sr1.jpg
image:sr1.jpg
The cone in the -t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
The geometry of Minkowski space can be depicted using Minkowski diagrams, which are also useful in understanding many of the thought-experiments in special relativity.
Related topics
- People: Arthur Eddington | Albert Einstein | Hendrik Lorentz | Hermann Minkowski | Bernhard Riemann | Henri Poincaré | Alexander MacFarlane | Harry Bateman | Robert S. Shankland
- Relativity: Theory of relativity | principle of relativity | general relativity | frame of reference | inertial frame of reference | Lorentz transformations
- Physics: Newtonian Mechanics | spacetime | speed of light | simultaneity | cosmology | Doppler effect | relativistic Euler equations | Aether drag hypothesis
- Math: Minkowski space | four-vector | world line | light cone | Lorentz group | Poincaré group | geometry | tensors | split-complex number
- Philosophy: actualism | convensionalism | formalism
External links
Template:Wikibookspar Template:Wikibookspar
- Relativity calculator (http://www.magen.co.uk/calculator.html) Geometric calculations of relativistic problems such as the addition of velocities. Note that it is Java-based and can take several minutes to load using a 56k modem.
- Relativity in its Historical Context (http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Special_relativity.html) The discovery of special relativity was inevitable, given the momentous discoveries that preceded it.
- Nothing but Relativity (http://arxiv.org/PS_cache/physics/pdf/0302/0302045.pdf) There are many ways to derive the Lorentz transformation without invoking Einstein's constancy of light postulate. The path preferred in this paper restates a simple, established approach.
- Reflections on Relativity (http://www.mathpages.com/rr/rrtoc.htm) A complete online book on relativity
- Synchronization Gauges and the Principles of Special Relativity (http://arxiv.org/abs/gr-qc/0409105) The principles of Special Relativity Theory (SRT) allow for a wide range of ‘theories’ that differ from the standard SRT only for the difference in the chosen synchronization procedures, but are wholly equivalent to SRT in predicting empirical facts. 57 pages.
- Quaternions in University-Level Physics Considering Special Relativity (http://arxiv.org/ftp/physics/papers/0308/0308017.pdf) The quaternions are an expansion of complex numbers and show close relations to numerous physically fundamental concepts (e.g. Pauli Matrices).
- Imaginary in all directions (http://arxiv.org/PS_cache/math-ph/pdf/0309/0309061.pdf) There is a preferred algebra of quaternions and complex numbers that is ideally suited to express the equations of special relativity and classical electrodynamics.
- Special Relativity Lecture Notes (http://www.phys.vt.edu/~takeuchi/relativity/notes) A standard introduction to special relativity where explanations are based on pictures called spacetime diagrams.
- Brane World Mach Principles and the Michelson-Morley experiment (http://www.mathpreprints.com/math/Preprint/paultrr/20040119/1/Evaluation_of_Brane_World_Mach_Principles.pdf)
- Why Hyperspace & Dual Reference frames (http://doc.cern.ch//archive/electronic/other/ext/ext-2004-121.pdf)
- Petites expériences de pensée (http://fr.wikipedia.org/wiki/Relativit%C3%A9_restreinte#Petites_exp.C3.A9riences_de_pens.C3.A9e) : five interesting thought experiments about special relativity quoted in the French Language Wikipedia.
- Special relativity theory made intuitive (http://spoirier.lautre.net/en/relativity.htm) : a new approach to explain the theoretical meaning of Special Relativity from an intuitive geometrical viewpoint
- Special Relativity (http://www2.slac.stanford.edu/vvc/theory/relativity.html) Stanford University, Helen Quinn, 2003
- Template:Gutenberg, by Albert Einstein
- Special Relativity (http://www.motionmountain.net/C-2-CLSC.pdf) This is chapter two of Christoph Schiller's 1000 page walk through the whole of physics, from classical mechanics to relativity, electrodynamics, thermodynamics, quantum theory, nuclear physics and unification. 61 pages.
- University Lectures on Special Relativity (http://www.physics.mq.edu.au/~jcresser/Phys378/LectureNotes/SpecialRelativityNotes.pdf) Lecture notes on Special Relativity, prepared by J. D. Cresser, Department of Physics, Macquarie University. 44 pages.
- "Why Einstein may have got it wrong" (http://www.guardian.co.uk/life/science/story/0,12996,1456747,00.html) by David Adam, The Guardian, April 11, 2005.
- Through Einstein's Eyes (http://www.anu.edu.au/Physics/Savage/TEE/) The Australian National University. Relativistic visual effects explained with movies and images.
- Greg Egan's Foundations (http://gregegan.customer.netspace.net.au/FOUNDATIONS/01/found01.html).
- Short Essay Explaining Special Relativity (http://3quarksdaily.blogs.com/3quarksdaily/2005/06/monday_musing_s.html) by S. Abbas Raza of 3 Quarks Daily (http://3quarksdaily.com)
References
- On the Electrodynamics of Moving Bodies (http://www.fourmilab.ch/etexts/einstein/specrel/www/), A. Einstein, Annalen der Physik, 17:891, June 30, 1905 (in English translation)
- Einstein, Albert. The Meaning of Relativity.
- Schutz, Bernard F. A First Course in General Relativity, Cambridge University Press.
- Taylor, Edwin, and Wheeler, John, Spacetime physics, W.H. Freeman and Company, second edition, 1992.
- Wolf, Peter and Gerard, Petit. "Satellite test of Special Relativity using the Global Positioning System," Physics Review A 56 (6), 4405-4409 (1997).
- Will, Clifford M. "Clock synchronization and isotropy of the one-way speed of light," Physics Review D 45, 403-411 (1992).
- Alvager et al., "Test of the Second Postulate of Special Relativity in the GeV region," Physics Letters 12, 260 (1964).
| General subfields within physics | |
|
Classical mechanics | Condensed matter physics | Continuum mechanics | Electromagnetism | General relativity | Particle physics | Quantum field theory | Quantum mechanics | Solid state physics | Special relativity | Statistical mechanics | Thermodynamics | |
cs:Speciální teorie relativity da:Speciel relativitetsteori de:Spezielle Relativitätstheorie es:Relatividad especial fr:Relativité restreinte ko:특수 상대성 이론 ia:Relativitate special it:Relatività ristretta he:תורת היחסות הפרטית la:Relativitas specialis lt:Specialioji reliatyvumo teorija hu:Speciális relativitáselmélet nl:Speciale relativiteitstheorie ja:特殊相対性理論 pl:Szczególna teoria względności pt:Relatividade restrita ru:Специальная теория относительности sk:Špeciálna teória relativity sl:Posebna teorija relativnosti fi:Erityinen suhteellisuusteoria sv:Speciella relativitetsteorin tl:Espesyal na relativity tt:Maxsus çağıştırmalılıq teorise vi:Thuyết tương đối hẹp